research
Universal visitation law of human mobility

Human mobility patterns are surprisingly simple. In spite of many hard to model effects like socioeconomic activities, enviromental conditions, and individual preferences, net migration flows between different locations obey a universal “radiation” model. Here we show that the spectrum of these flows – defined as the number of individuals that visit a given location with frequency f from a distance r away – are also universal: they obey a simple inverse square law in the product rf.
- Universal visitation law of human mobility Nature, 593, 522-527 (2021)
- Visualization
The sensing power of vehicle fleets

Monitoring urban environments is a challenging task; air pollution, road quality, congestion, and other quantities of interest vary widely across both time and space, requiring much effort to accurately monitor. Here we show attaching sensors to third party urban vehicles – like cars, taxis, buses or trucks – could offer a cheap and scalable solution to this problem.
- Quantifying the sensing power of vehicle fleets PNAS 116.26 (2019)
- Visualization
Swarmalators: oscillators that sync and swarm
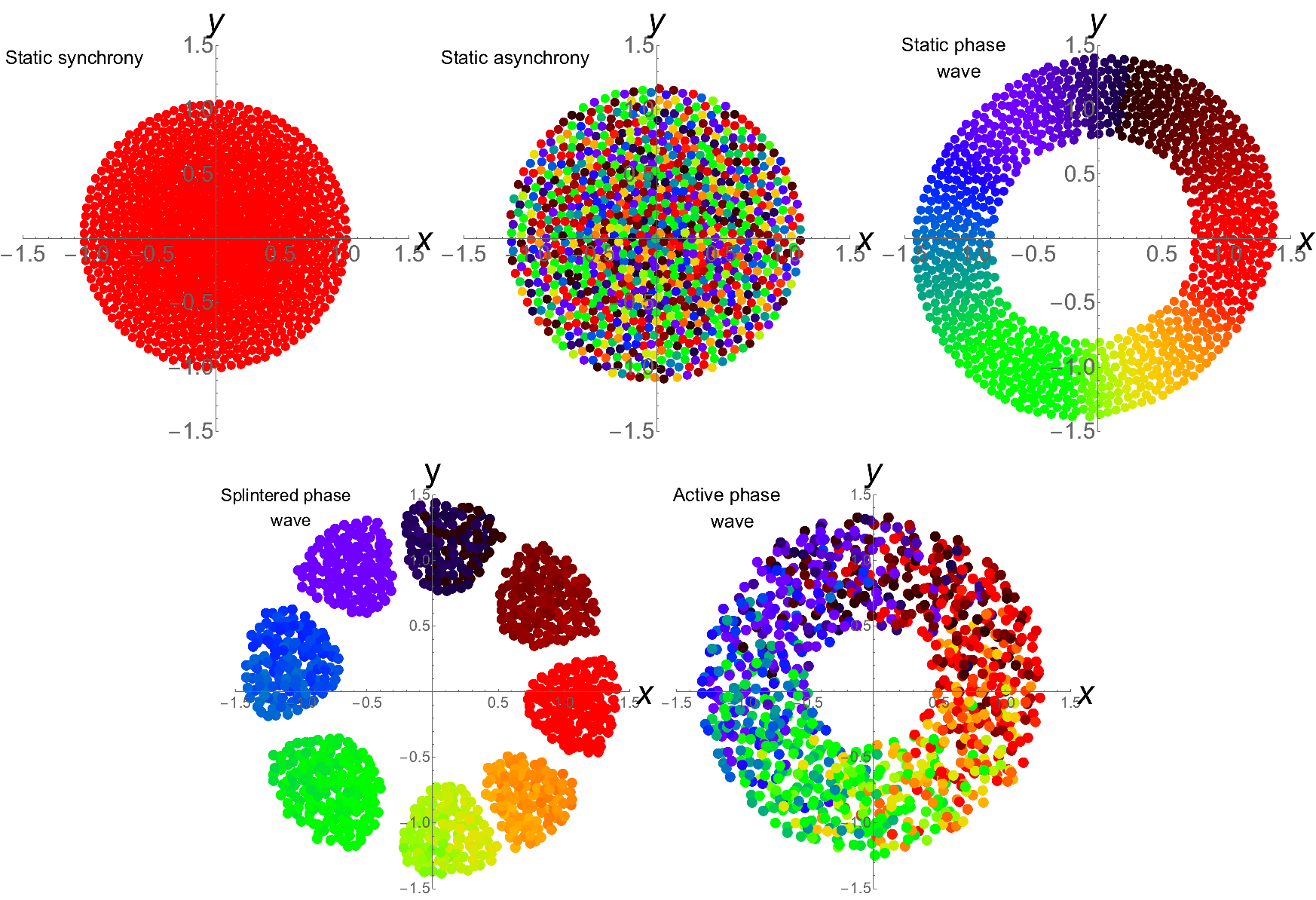
Clocks, hearts, and lasers synchronize their behavior in time. Birds, fish, and insects swarm as groups in space. This project is about entities which both sync and swarm, spontaneously self-organizing in both space and time. Examples of “swarmalators” – or swarming oscillators – include sperm, Janus particles, and tree frogs.
Swarmalators have been realized in the lab (2D, 2D, 3D) and been used as inspiration for making music!
- Oscillators that sync and swarm Nature Communications 8.1 (2017)
- Visualizations here and here
- Python code & Mathematica code
Pulse coupled oscillators

During every heartbeat, thousands of pacemaker cells discharge all-at-once. This collective firing contracs the cardiac muscles which pumps blood around the body. This paper studies how the cells manage to synchronize their discharges – how they keep the heart beating.
- Cluster Kinetics of Pulse-Coupled Oscillators Physical Review Letters 115.6 (2015)
The curious tourist problem
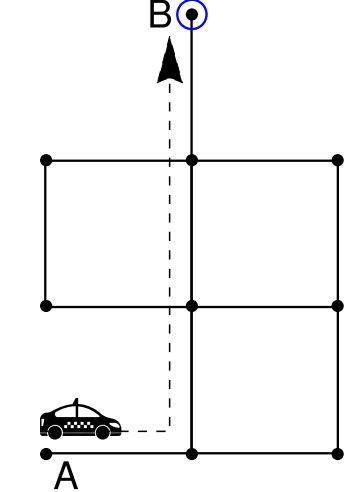
A puzzle for probability theorists:
A curious tourist arrives in a city with N roads arranged in a network G. She decides to explore the city by taking taxis to randomly chosen locations (via shortest paths). After being dropped off by a taxi at a given location, she is immediately picked up by another taxi and brought to a new location. How long does it take her to cover every road at least once? Here we numerically explore the curious tourist problem (and other aspects of the taxi-drive, the stochastic process implied by the puzzle), but an analytic solution remains elusive.
- Urban sensing as a random search problem Physica A 562 (2020)
- Code
The darkweb: a social network anomaly

The darkweb is unusual. About 87% of its sites never link to another site. To call it a “web” is thus a misnomer – it’s better described as a set of largely isolated dark silos. This topology is highly dissimilar to other social networks and indicates darkweb users behave much differently to www users. Preferential attachment can partially explain the strange topology of the darkweb, but a more accurate model based on the social behavior of its users is lacking.